基于分子动力学方法研究金属层合板轧制复合过程界面区材料的微观变形行为,从力学性能和位错运动的角度,对比研究双金属FeCrNi/Fe与单金属的压缩变形,揭示非共格界面对金属微观变形行为的影响。结果表明,双金属模型与2种单金属模型在应力-应变关系和变形行为规律方面都存在明显差异;由于复合界面的存在,变形过程中双金属模型纯Fe基体中的位错在界面附近积累,界面原子的局部剪切作用使FeCrNi基体中的位错形成变得容易,降低了FeCrNi基体的屈服强度;复合界面对于变形过程中位错传播的阻碍作用,使材料抵抗塑性变形的能力得到提高,变形过程中2种金属基体内位错密度的交替变化导致2种金属基体的变形量也对应呈现交替变化的特殊现象。
关键词:
轧制复合是目前金属层合板的主要制备方法,与爆炸焊等方法相比,具有复合质量高、生产效率高、安全便捷等优点[1,2,3]。轧制复合不锈钢-碳钢层合板时,上下轧辊旋转并以表面摩擦力驱动分离状态的各层金属带,依序快速完成复合的一系列连续工艺过程,包括各层金属带运动前进、被咬入辊缝、被轧制减薄乃至层间接触界面实现结合后离开辊缝。其中,在轧制减薄过程中,各层钢带因轧制发生剧烈塑性变形,使金属表面破裂,裸露出未氧化、无污染的新鲜本体材料,并在轧制压力作用下界面两侧表层材料相互接近到原子尺度的接触而产生两侧原子间键合以及原子跨界面扩散,从而实现不锈钢与碳钢的大面积固相复合。轧制减薄过程中基材的变形和接触是实现复合的基础工艺条件,界面原子的键合和扩散是实现复合的物理机制,实现界面间大面积类似冶金结合是复合的技术质量目标。轧制复合过程中各组元基材的变形协调性与其轧制工艺以及各基材的轧前初始厚度比和塑性本构有关,并严重影响复合质量与界面结合强度[4,5]。与扩散焊接和摩擦焊接轧制复合不同,轧制复合既有异种金属间原子的键合与扩散现象,还伴随着基材金属的剧烈塑性变形。因此,研究不锈钢与碳钢轧制复合理论与技术,除了需要仿真或实验研究复合变形过程中基材的弹塑性变形行为和实现复合的临界工艺条件,还需围绕界面层金属原子的运动与位错的演化,从微观尺度上探索不锈钢与碳钢轧制复合过程塑性变形行为。
势函数的选择是分子动力学模拟中的关键问题。目前,针对具有相同晶格结构双金属复合过程的模拟,已提出多个适用的势函数,模型及建模都较为成熟,并且已经针对fcc-fcc结构的Al-Fe、Cu-Fe、Fe-Ni和bcc-bcc结构的Cr-Fe等开展了相关研究,Mendelev等[11]开发了一种可以准确描述Al-Fe体扩散过程的势函数,基于此分析了Al中Fe杂质对晶界迁移的影响;Bonny等[12]开发了一种三元多体Fe-Cu-Ni势函数,并通过模拟退火实验对势函数进行了验证;Stukowski等[13]提出了更有效计算Cr-Fe体系中单个粒子位移/变形能的EAM (embedded-atom method)势函数。但是,针对具有不同晶格结构双金属复合过程的模拟,由于很难用一种势函数同时准确描述2种或者更多种晶格结构的材料,导致目前的各个势函数都不能获得理想的模拟结果,其适用性尚难以评价比较。
在双金属或多金属复合材料塑性变形过程中,界面有着重要的影响。界面既可以阻碍位错运动,也是位错的发射源[14,15,16]。近年来,国内外学者利用分子动力学方法,针对界面对多层金属的塑性变形影响机理开展了广泛的研究,Shao和Medyanik[17]模拟了非共格界面的Cu/Nb双金属在纳米压痕仪作用下位错的增殖和演化行为,研究了不同加载过程中变形机理的差异;Wang等[18]用相似的方法进行了研究,认为在Cu/Nb非共格界面系统中界面会阻碍滑移位错的发射;Misra等[19]同样针对Cu/Nb双金属利用分子动力学方法进行变形模拟,发现在界面位置存在局部原子的剪切作用,在界面处出现滑移位错和位错核的扩散;Weng等[20]通过模拟半共格、共格、非共格3种界面类型Cu/Ni双金属的拉伸过程,分析了界面类型对位错运动以及材料力学性能的影响。罗旋等[21]研究了Ag/Ni和Cu/Ni失配位错程度对界面力学性能的影响;程东等[22]模拟了Cu/Ni金属在纳米压入和微摩擦过程中位错的运动规律,认为界面失配位错网对位错运动的排斥阻力以及由弹性模量差而产生的界面镜像力是位错被限制在Cu层的微观机理;成聪等[23]研究了Cu/Ni双金属在不同应变率下进行应变加载时的变形机理,发现应变率的增加有利于纳米多晶结构中堆垛层错原子团的增加,从而造成材料屈服强度的增加。上述研究主要从位错运动的角度分析界面类型对材料力学性能的影响,而双金属内部位错密度变化规律以及对材料变形的影响并未涉及。本工作在建立了不同晶格结构金属轧制复合模型后,利用分子动力学方法模拟FeCrNi/Fe、Fe与FeCrNi轧制变形过程,对比其变形行为及规律,研究整个变形阶段位错密度变化规律及其对变形的影响,探究非共格界面对于金属塑性变形行为的影响。
势函数的适用性是经典分子动力学模拟首先要解决的关键问题。构建可靠的势函数,需要针对具体体系进行参数拟合,因此拟合好的势函数原则上只能用于被拟合的特定体系。而在解决实际问题的模拟过程中,所模拟体系的元素含量、晶格结构等不一定与该特定体系完全一致,需要对势函数的适用性进行验证。
因此,本工作提出如下评价比较势函数在模拟双金属轧制复合过程的适用性的方法及其定量指标:首先,体系中势能最小意味着晶格的最稳定状态,因此将能量最小时的晶格常数与实验中晶格常数实测值的一致性作为势函数适用性的第一个评价指标;其次,体系中参与构成正常晶格结构的原子越多则材料的微观结构越稳定,因此针对目前采用一种势函数模拟2种不同晶格类型材料时出现的部分原子紊乱现象,通过考察弛豫过程中原子结构的稳定性,定义正常晶格原子占总原子之比为晶格保持度,并以此作为势函数适用性的第二个评价指标;最后,针对轧制复合实际问题进行分子动力学方法建模和模拟计算,模拟研究具有不同晶格结构的双金属基材轧制复合过程,计算其晶格常数一致性和晶格保持度,并验证上述分子动力学模拟的势函数适用性评价标准。
304不锈钢是具有典型fcc结构的奥氏体钢,其主要成分是Fe、Cr、Ni,同时还含有微量的Mn、Nb、Mo、Ti、N等元素,其中Cr含量(质量分数,下同)为17%~19%,Ni含量8%~10%,忽略其中的微量合金元素,则Fe17Cr5Ni2与AISI-304奥氏体不锈钢成分接近。首先建立含16384个原子的fcc-Fe模型,然后分别用Cr原子、Ni原子按一定比例随机取代Fe原子建立304不锈钢的初始模型,比例为Fe∶Cr∶Ni=17∶5∶2。Q235碳钢为bcc结构,其主要成分是Fe,因此采用bcc-Fe模拟Q235碳钢材料。
图1 FeCrNi/Fe在势函数1和势函数2下驰豫过程中的结构含量
Fig.1 Contents of various lattice structures of FeCrNi/Fe in the relaxation process with potential function 1 (a) and potential function 2 (b) (The green, red and blue colors represent the fcc, hcp and bcc atoms, respectively)
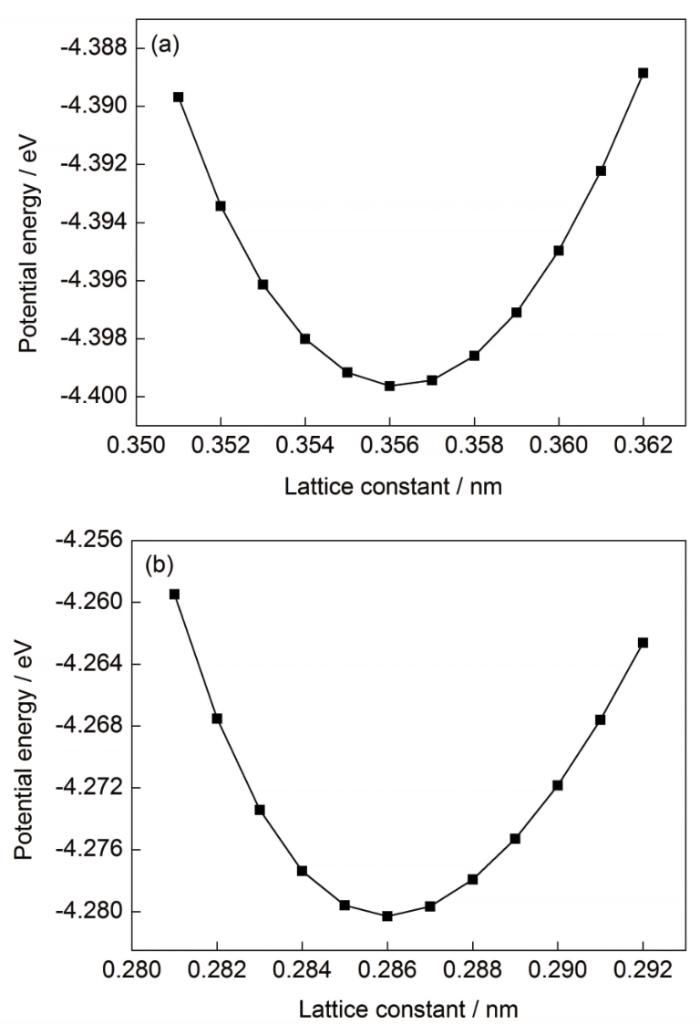
图2 势函数1作用下不同晶格常数FeCrNi和Fe的势能变化
Fig.2 Potential energies of FeCrNi (a) and Fe (b) under different lattice constants with potential function 1
综上可知,利用分子动力学方法模拟金属轧制复合过程时,对于具有不同晶格结构的工况,本工作提出的以稳定状态下晶格常数的一致性和晶格结构的保持度作为评价标准选择确定最合适的势函数,是一种简单可行的近似解决方法。
图3 FeCrNi/Fe模型、FeCrNi模型和Fe模型的初始构型
Fig.3 Initial configurations of FeCrNi/Fe (a), FeCrNi (b) and Fe (c)
对3种模型进行压缩过程模拟,在600 K下沿z轴即[001]方向对样品进行均匀压缩,每步施加0.003的压缩应变,直到应变为0.6为止。为了对比变形过程中3种模型的力学性能和讨论压缩过程中位错的演化,以及分析力学性能出现差异的原因,采用位错提取法(dislocation extraction algorithm,DXA)[28]对变形过程中位错线总长度的变化进行定量化的统计。该方法依赖CNA技术来识别出位于位错核的原子,然后基于拓扑连通性将这些原子组装成位错线分量,采用Burgers回路方法决定位错线分量的Burgers矢量。
最后结合不锈钢/碳钢热压缩复合过程中的宏观变形规律,讨论分析分子动力学模拟所得的双金属微观变形规律。
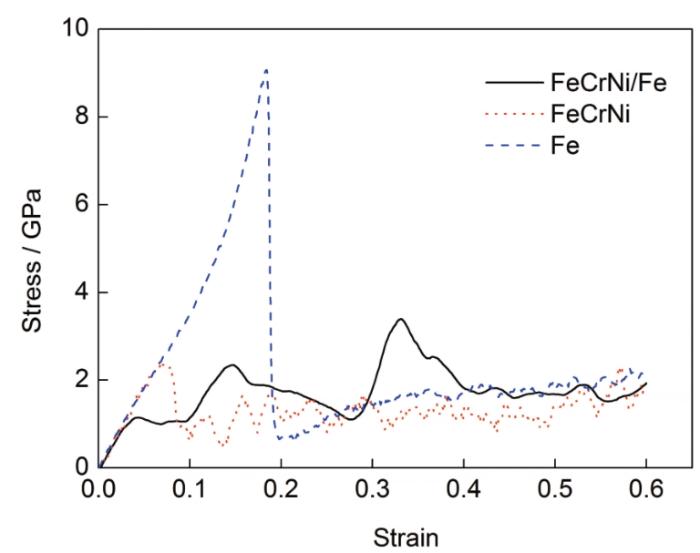
FeCrNi/Fe、FeCrNi、Fe 3种材料热压缩过程中微观尺度上的应力-应变曲线如图4所示。可以看出,在应力达到第一个峰值之前材料处于弹性变形阶段,在该阶段应力随着应变线性增加,FeCrNi/Fe、FeCrNi和Fe的压缩应变分别达到0.05、0.072、0.18时各自出现应力的第一个峰值,随后开始进入塑性变形阶段。3种材料压缩过程中的弹性模量相同但屈服强度存在差异,其中FeCrNi/Fe的屈服强度最小,为1.15 GPa,FeCrNi、纯Fe变形过程中屈服强度分别为2.37和9.07 GPa。此外,3种材料在塑性变形阶段的变形形式也有所不同,FeCrNi、纯Fe材料的应力在屈服点之后迅速下降,应力-应变曲线逐渐平缓,应力呈锯齿状的缓慢波动,而FeCrNi/Fe材料的应力-应变曲线在屈服点后开始大幅波动,应变达到0.4左右时应力才逐渐趋于平稳。
图4 双金属FeCrNi/Fe、单金属FeCrNi和Fe沿z方向压缩的应力-应变曲线
Fig.4 Stress-strain curves for FeCrNi/Fe、FeCrNi and Fe under z-direction compression
但是,从数值上看,分子动力学模拟所得到的流变应力远大于通过宏观唯象实验实测得到的应力,而且大了1~2个数量级。这可能是由于分子动力学模型对金属材料晶体进行了无缺陷理想化假设,并且只是极小规模原子数的原子尺度建模和模拟所导致的误差,但也是该方法目前尚难克服的不足。
2.3.1 双金属中的FeCrNi基体中位错的产生与演化
FeCrNi/Fe双金属在变形过程中的应力-应变曲线及不同应变时的变形截图如图5所示,FeCrNi基体内部位错的产生及发射过程如图6所示。由于双金属界面为非共格界面,因此在弛豫结束后碳钢基体(模型上半部分)内有大量位错线产生,随着应变增加至A点,FeCrNi基体靠近界面处开始有位错出现,这意味着FeCrNi基体开始塑性变形。位错的出现使原子间的运动变得更加容易,即要达到相同变形量时需要的应力较小,这也是应力-应变曲线开始下降的原因。不全位错滑移后产生FeCrNi基体原子的错排并留下堆垛层错。随后次级位错开动,在滑移面上拓展并相互交错形成Hirth阻塞。由于位错发射路径的一侧存在堆垛层错,一部分位错被堆垛层错俘获而被永久固定住,位错只能沿另一侧发射,使得位错的可动性降低,引起宏观上材料的加工硬化现象。
图5 600 K下FeCrNi/Fe沿z方向单轴压缩作用下的应力-应变曲线以及材料变形截图
Fig.5 Stress-strain curve and the sequence of snapshots capturing the atomic deformation process for FeCrNi/Fe under z-direction uniaxial compression at 600 K (The red, blue and yellow colors represent the Fe, Cr and Ni atoms, respectively, in FeCrNi matrix. The white color represents the Fe atoms in Fe matrix)
图6 图5中A~B阶段,变形过程中界面处位错向FeCrNi基体发射过程
Fig.6 Atomic configurations (a1, b1, a2, b2) and dislocation distributions (c1, c2) at point A (a1~c1) and point B (a2~c2) in Fig.5 showing the process of dislocation at the interface emitted to the FeCrNi matrix (Red color represents the hcp atoms and two adjacent hcp atoms mean an intrinsic stacking fault)
与FeCrNi、Fe相比,FeCrNi/Fe变形过程中的屈服强度最小,对于非共格界面,由于晶格常数的失配以及不同金属晶格结构存在差异,界面对位错起到阻碍和吸收作用,使得位错在变形过程中不能穿过界面。另一方面,位错在界面积累,造成界面的弱化和局部剪切效应[20]。FeCrNi/Fe模型中纯Fe基体内部的位错在界面处积累,界面处FeCrNi基体原子的局部剪切效应使得位错的形成相比FeCrNi模型更加容易,FeCrNi基体塑性变形也变得更加容易,从而降低了FeCrNi基体的屈服强度。
2.3.2 双金属的纯Fe基体中位错的演化与消失
如图7所示,在应变到达0.05 (A点)之后,FeCrNi基体开始发生变形的同时,由于FeCrNi和Fe基体变形的相互协调作用,纯Fe基体内部位错塞积开动,材料内部变形应力使纯Fe基体部分原子在剪切作用下出现原子重排的现象。纯Fe基体内位错密度逐渐减小,造成B~C阶段应力-应变曲线略有上升的趋势。随着应变增大至0.096 (C点),纯Fe基体内部位错线基本消失。晶粒取向趋于与压缩方向一致,纯Fe基体原子重排完成。
图7 图5中A~C阶段变形过程中纯Fe基体内部原子重排过程
Fig.7 Atomic configurations at point A (a), point B (b) and point C (c) in Fig.5 showing the process of atoms rearrangement of Fe matrix
2.3.3 双金属与单金属变形过程中位错演变规律对比分析
双金属FeCrNi/Fe变形过程中材料位错密度分布情况如图8a1~f1所示。可见,A~C阶段,FeCrNi基体内部位错产生并逐渐增多,与此同时纯Fe基体内部发生原子重排,位错逐渐减少。C~D阶段,FeCrNi基体内部位错形核速率大于湮灭速率,位错密度逐渐增大形成位错塞积,位错之间产生交互作用,造成应力-应变曲线的上升。该阶段FeCrNi/Fe的变形以FeCrNi基体的变形为主。与此同时,纯Fe基体内部也有少量的位错出现。D点以后FeCrNi基体由于位错的塞积到了一定程度,FeCrNi基体进一步变形变得困难,纯Fe基体又开始有不完全位错出现,位错在界面处以及顶部出现并向基体部分发射,该阶段FeCrNi/Fe的变形主要以Fe基体的变形为主。E~F阶段,应力上升的机理与B~C阶段类似,是由于FeCrNi基体原子的重排所致。
图8 双金属FeCrNi/Fe和单金属FeCrNi变形过程中的位错演化
Fig.8 Dislocation distributions of FeCrNi/Fe at points A~F in Fig.5, respectively, during deformation (a1~f1) and dislocation distributions of FeCrNi when the strain is 0.078, 0.1, 0.2 and 0.3, respectively (a2~d2)
可以看出,在FeCrNi和Fe基体中,整个变形过程中位错密度呈现交替变化的规律。A~D阶段,纯Fe基体位错密度的增加伴随着不锈钢位错密度的减小;而D~F阶段,FeCrNi基体位错密度减小伴随着纯Fe基体位错密度的增加。分子动力学方法模拟FeCrNi模型单金属变形过程位错演化过程如图8a2~d2所示。与变形过程中双金属基体的位错演化规律对比可以看出,双金属塑性变形阶段与单一金属相比存在很大差异,随着应变的增加,FeCrNi模型材料内位错线是始终存在的。
由于界面对位错的阻碍作用,使位错密度在基体中增大,同时界面处不断积累的位错产生的局部剪切作用又引起另一基体内部原子的重排,造成其位错密度减小,形成应力-应变曲线的多峰形状。与单金属相比,变形过程中双金属原子的运动也变得困难,在塑性变形过程中抵抗塑性变形的能力得到增强。
众所周知,位错的滑移是金属的主要塑性变形机制,位错的累积运动导致宏观的塑性变形。位错塞积使得金属的塑性变形变得困难,而位错塞积的开动则有利于金属的进一步变形。根据Zepeda-Ruiz等[6]的研究,整个流动的金属体可以被视作一个保持稳定能量耗散速率的开放热力学系统,该系统的机械能通过应变提供,接着通过位错的增殖、湮灭、运动转换为热能,而材料的内部状态(饱和流动应力、位错密度)和外界应变条件(温度、压力、应变等)是唯一关联的。在变形过程中,双金属两基体的厚度及总位错线长度随应变的变化规律如图9所示,其中图9a中各个阶段厚度的变化率代表着材料的变形能力,在双金属的变形过程,微观尺度上总位错线长度的交替变化使得两基体的变形能力时刻发生着改变。
图9 双金属FeCrNi/Fe两基体的厚度和总位错线长度随应变的变化
Fig.9 Thicknesses (a) and lengths of the total dislocation line (b) of two matrices of FeCrNi/Fe under different strains
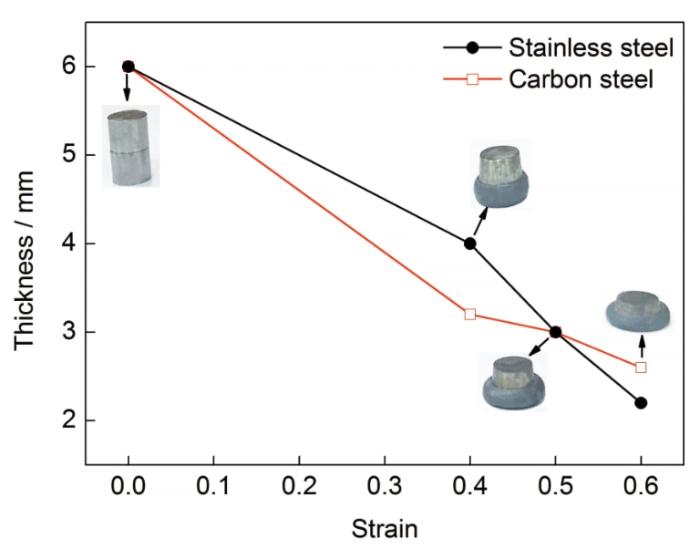
为研究双金属位错演化对宏观变形的影响,利用Gleeble3500试验机在600 K下对AISI 304不锈钢和Q235A碳钢进行热压缩变形,材料为直径8 mm、长6 mm圆柱形试样,不同压下率下不锈钢和碳钢的厚度变化如图10所示。变形开始时,由于碳钢的塑性变形能力大于不锈钢,双金属的变形主要以碳钢的变形为主,随着变形的继续,碳钢基体内位错密度逐渐增加,变形因而变得困难,不锈钢的变形能力大于碳钢,应变为0.5时两基体厚度基本一致,随后不锈钢的变形量开始超过碳钢。可以看出,随着压下量的不断增大,不锈钢和碳钢基体的厚度与模拟过程中总位错线长度均呈现出交替变化的趋势。根据本工作对双金属FeCrNi/Fe变形过程中位错密度演变的模拟结果,可以认为界面两侧位错密度的交替变化是引起两基体交替变形的原因。
图10 静压实验过程中各基材厚度的变化
Fig.10 Thickness variations of two base metals during deformation bonding process
(1) 针对具有不同晶格结构的2种金属基材轧制复合变形过程,通过基于实际问题的建模和模拟计算,提出了以稳定状态下晶格常数的准确度及晶格结构的保持度作为势函数适用性的评价标准以及相应针对不同晶格结构材料势函数选择确定方法,建立了一种利用分子动力学方法模拟不同晶格结构多金属材料弹塑性变形过程中势函数选择确定的近似解决办法。
(2) 应用分子动力学方法建模及模拟不同晶格结构的FeCrNi/Fe复合过程,研究了界面对双金属塑性变形过程的影响,并通过与相同工况条件下单金属变形行为进行对比,初步探索了双金属轧制复合过程微观塑性变形行为及规律。
(3) 对于非共格界面,复合过程中位错更容易在界面处形核,并使材料更容易发生变形;界面对位错运动的阻碍作用增加了双金属抵抗塑性变形的能力;压缩变形过程中,双金属模型2种材料位错密度的交替变化导致了各自变形量的交替变化。
1 不同晶格结构金属轧制复合模型的建立
1.1 势函数的适用性验证指标
1.2 不同晶格结构的不锈钢/碳钢轧制复合模型
图1

图2
2 非共格界面金属轧制复合微观变形模拟分析
2.1 建模及模拟
图3

2.2 变形过程应力-应变关系对比分析
图4
2.3 变形过程中位错演变规律比较分析
图5

图6
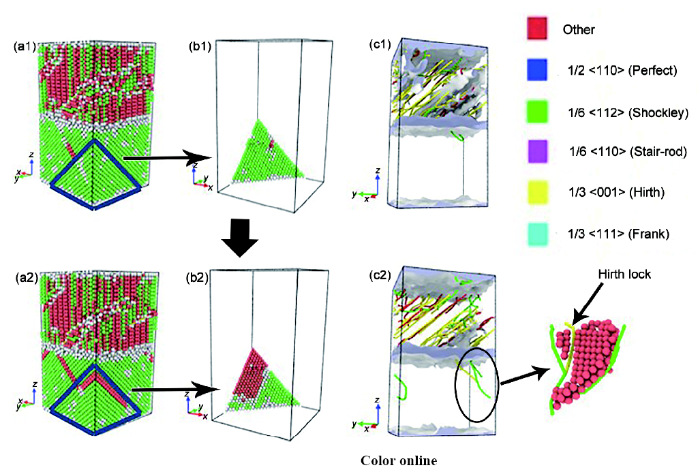
图7

图8

2.4 实验对比及验证
图9

图10
3 结论
来源--金属学报
国检检测最新产品
同类文章排行
- 分享:
- 分享:金属轧制复合过程微观变形行为的分子动力学建模及研究
- 分享:B4C/6061Al复合材料热压缩断裂行为的多尺度研究
- 分享:新型耐磨耐高温氧化NiCrAlSiC复合涂层的制备及性能研究
- 分享:GH984G合金在700 ℃水蒸气中的氧化行为
- 分享:Al-Bi合金凝固过程及微合金化元素Sn的影响
- 分享:Mo元素及热处理对Ni2CrFeMox高熵合金在NaCl溶液中耐蚀性能的影响
- 分享:地质处置低氧过渡期X65低碳钢腐蚀行为研究
- 分享:静水压力对超纯Fe腐蚀行为的影响
- 分享:电磁旋流水口连铸技术对小方坯凝固组织形貌和宏观偏析的影响
最新资讯文章
您的浏览历史










 沪公网安备31011202020290号
沪公网安备31011202020290号
